Classifying toxicity of antisense oligonucleotides

by: Meera Machado & Lykke Pedersen

Feyn version: 2.0.+

Why use a QLattice?

The QLattice is a quantum-inspired algorithm that explores the space of all mathematical expressions that relate the output (toxicity) to the input (ASO characteristics). The result of the search is a list of hypotheses sorted by how well they match observations. Caspase toxicity is a biological mechanism that is a function of many cellular subprocesses. We engineered some simple features and allowed the QLattice to search through different interactions between them that describe toxicity. The result in the end is not only a predictive model that we can benchmark, but an actual explanation towards the underlying biology that enables us to design less toxic compounds in the future.

Data

In our analysis, we used the data from [Papargyri et al][https://doi.org/10.1016/j.omtn.2019.12.011]. The data set contains two sets of iso-sequential LNA gapmers, where the authors of the study systematically varied the number and positions of LNA modifications in the flanks. Specifically, there are 768 different LNA gapmers, where 386 of them target a region we will call region A, and 386 of them target a region we will call region B. This means the “6mer-gap” is the same within each region and the only variance is in the flanks. Four of the ASOs target neither of the regions and were included in the original study as inactive controls. We will not use those four ASOs here.

In the aforementioned study toxicity is measured by caspase activation. Below are five entries of the data set:

# R

# Required R-packages for running this guide
library(tidyverse) # data manipulation
library(reticulate) # running python in R
library(knitr) # nice tables in Rmd with kable()
library(htmltools) # embedding html in Rmd
library(pROC) # plotting ROC curves

# reading in the caspase data
tab = read_csv('../data/aso.csv')

# the head of the data table
head(tab) %>%
  kable()
target sequence design cas_avg kd_avg
P GCaagcatcctGT LLDDDDDDDDDLL 285.3819 25.50086
P GTTactgccttcTTAc LLLDDDDDDDDDLLLD 185.4886 27.14577
C TTGaataagtggaTGT LLLDDDDDDDDDDLLL 113.4227 78.17622
C CcAAAtcttataataACtAC LDLLLDDDDDDDDDDLLDLL 163.3720 78.08273
A TGGCaagcatccTGTA LLLLDDDDDDDDLLLL 348.9665 88.27147
A TGGCAagcatcCTGTA LLLLLDDDDDDLLLLL 444.7894 81.58408
  • target: A or B, indicates which region in HIF1A is targeted;
  • sequence: the camelcase sequence of the ASO. Lowercase means DNA, uppercase means LNA;
  • design: the gapmer design. Each character is either L or D for LNA or DNA;
  • cas_avg: the average caspase activation across several measurements; and
  • kd_avg: average knockdown of the ASO.

QLattice in R

To run the QLattice inside R you need to have python (>v3.7) installed and also the reticulate package in R. The R-chunk below shows how to install the required python modules.

# R

# pointing R to the correct python installation
path_to_python = Sys.which("python3")
reticulate::use_python(path_to_python)

Feature engineering

First we will use the QLattice to find a mathematical expression that will serve as a hypothesis for the relation between LNA ASO design and toxicity solely on region A. The key point of a hypothesis is to be able to invalidate it. Along these lines, we will scrutinize this hypothesis by testing whether it generalises to region B.

Previous work has shown that a reasonable threshold for caspase activation is 300% ([Dieckmann et al][https://doi.org/10.1016/j.omtn.2017.11.004]).

We will use this as the cutoff value for training a QLattice classification model: below this value the drug is seen as having low/mid levels of toxicity (negative class), while above this threshold the drug is seen as (very) toxic (positive class).

We will engineer four features that capture some of the LNA ASOs design:

  • lna_5p: the number of LNA sugars in the left flank (5’);
  • lna_3p: the number of LNA sugars in the right flank (3’);
  • lna_count: the number of LNA sugars across the ASO;
  • dna_count: the number of DNA sugars across the ASO; and
  • aso_len: the length of the ASO.
# R

# adding engineered features to tab by using mutate()
tab =
  mutate( tab,
    lna_5p = map_dbl(design, function(x){
      sum(unlist(strsplit(x,''))[1:5] == 'L')
    }),
    lna_3p = map_dbl(design, function(x){
      ii <- nchar(x)
      sum(unlist(strsplit(x,''))[(ii-5):ii] == 'L')
    }),
    lna_count = map_dbl(design, function(x){
      sum(unlist(strsplit(x,'')) == 'L')
    }),
    aso_len = nchar(design),
    dna_count = aso_len-lna_count,
    too_toxic = cas_avg > 300)

head(tab) %>%
  kable()
target sequence design cas_avg kd_avg lna_5p lna_3p lna_count aso_len dna_count too_toxic
P GCaagcatcctGT LLDDDDDDDDDLL 285.3819 25.50086 2 2 4 13 9 FALSE
P GTTactgccttcTTAc LLLDDDDDDDDDLLLD 185.4886 27.14577 3 3 6 16 10 FALSE
C TTGaataagtggaTGT LLLDDDDDDDDDDLLL 113.4227 78.17622 3 3 6 16 10 FALSE
C CcAAAtcttataataACtAC LDLLLDDDDDDDDDDLLDLL 163.3720 78.08273 4 4 8 20 12 FALSE
A TGGCaagcatccTGTA LLLLDDDDDDDDLLLL 348.9665 88.27147 4 4 8 16 8 TRUE
A TGGCAagcatcCTGTA LLLLLDDDDDDLLLLL 444.7894 81.58408 5 5 10 16 6 TRUE

Using QLattice for classification

In this tutorial we use the QLattice to generate classification models. Mathematically, this means that the QLattice will wrap each expression in a logistic function. This allows the output to be interpreted as a probability. In other words, if X is an input vector and Y is the event we want to predict, then the QLattice will search for functions f(X) such that the predictive power of

Y^=11+e−f(X)\hat Y = \frac{1}{1+e^{-f(X)}} is maximised.

In our case, Y is the probability of an ASO being above the 300% toxicity cutoff value, and f is any function of our input features. Specifically, the QLattice will be searching for the following expressions:

P^(tootoxic)=11+e−f(lna_5p,lna_3p,dna_count,lna_count,aso_len)\hat P (too_{toxic}) = \frac{1}{1+e^{-f(lna\_5p,lna\_3p,dna\_count, lna\_count, aso\_len)}}

Finding hypotheses

R-objects are embedded into python by calling r.{‘name of R-object’}. The below python chunk shows how to embed the R-object tab into python by calling r.tab and the split the data into a train and test set according to the target feature in tab.

# python

# importing modules
import pandas as pd
import feyn
import numpy as np
import matplotlib.pyplot as plt

# embed tab in python
tabP = r.tab
# split tab into train and test set
train = tabP[tabP.target == 'A']
test = tabP[tabP.target == 'B']

The training set displayed in R

# R
# head of train
head(py$train) %>% kable()
target sequence design cas_avg kd_avg lna_5p lna_3p lna_count aso_len dna_count too_toxic
4 A TGGCaagcatccTGTA LLLLDDDDDDDDLLLL 348.9665 88.27147 4 4 8 16 8 TRUE
5 A TGGCAagcatcCTGTA LLLLLDDDDDDLLLLL 444.7894 81.58408 5 5 10 16 6 TRUE
6 A TGGCaagcatcCTGTA LLLLDDDDDDDLLLLL 414.2047 77.24836 4 5 9 16 7 TRUE
7 A TGGcAagcatcCTGTA LLLDLDDDDDDLLLLL 536.3294 83.15933 4 5 9 16 7 TRUE
8 A TGGcaagcatcCTGTA LLLDDDDDDDDLLLLL 475.9408 74.90292 3 5 8 16 8 TRUE
9 A TGgCAagcatcCTGTA LLDLLDDDDDDLLLLL 477.3843 73.40393 4 5 9 16 7 TRUE

Below is a code snippet of how to search for hypotheses with the QLattice. Here we use Akaike information criterion (AIC) to sort the hypotheses. Also, train is the data set of region A we train the QLattice on.

#python

# Connecting to the QLattice
ql = feyn.connect_qlattice()

# Setting a seed
ql.reset(666)

features = ["lna_5p","lna_3p","lna_count", "dna_count", "aso_len", "too_toxic"]

# Sampling and fitting classification models
models = ql.auto_run(data=train[features],
                     output_name="too_toxic",
                     kind="classification",
                     max_complexity=7,
                     criterion="aic")

## Epoch no. 1 - Tried 2136 models - Best loss: 5.15e-01
## Epoch no. 2 - Tried 4159 models - Best loss: 5.01e-01
## Epoch no. 3 - Tried 5967 models - Best loss: 4.99e-01
## Epoch no. 4 - Tried 7676 models - Best loss: 4.98e-01
## Epoch no. 5 - Tried 9432 models - Best loss: 4.98e-01
## Epoch no. 6 - Tried 11226 models - Best loss: 5.02e-01
## Epoch no. 7 - Tried 13052 models - Best loss: 5.00e-01
## Epoch no. 8 - Tried 14773 models - Best loss: 4.99e-01
## Epoch no. 9 - Tried 16461 models - Best loss: 4.98e-01
## Epoch no. 10 - Tried 18082 models - Best loss: 4.97e-01

Results

Here is the best performing model according to AIC:

#python

# Getting best model
best_model = models[0]

This is the model represented as a graph object:

Loss: 4.97E-01(1, -1, -1) lna_3p linear: scale=0.500000 w=-1.335878 bias=1.1642lna_3p0num(0, -1, -1) lna_5p linear: scale=0.500000 w=1.619305 bias=-1.0238lna_5p1num(31, 2, 2) cell:squared(i)->isquared2x0(31, 1, 2) cell:squared(i)->isquared3x0(32, 2, 2) cell:add(i,i)->iadd4x0x1(33, 1, 3) too_toxic logistic: w=0.6718 bias=-1.2476too_toxi..5out

and this is the model interpreted as a mathematical expression:

# python

# displaying mathematical equation by use of sympify()
best_model.sympify(symbolic_lr =True)

## 1/(3.48212*exp(-0.910511*(1 - 0.573756*lna3p)**2 - 0.704222*(0.790818*lna5p - 1)**2) + 1)

The equation above sets the boundary between the positive and negative classes in the two-dimensional plane of lna_3p and lna_5p. We can see this demonstrated below where the colour bar is the probability of the ASO being too toxic.

# python

ax = best_model.plot_partial2d(train)
plt.show()

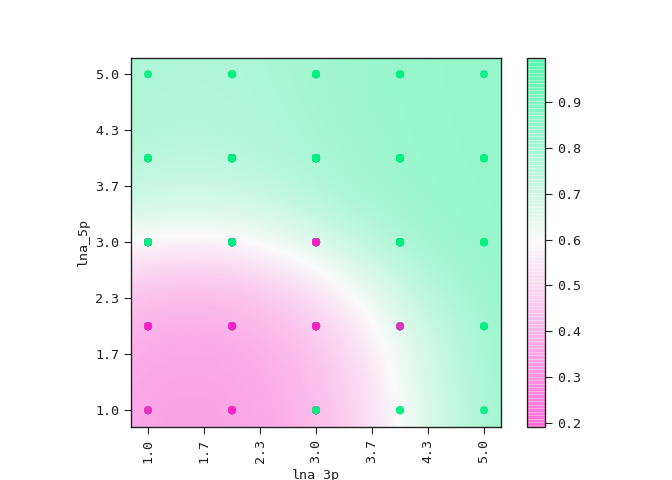Observe how the amount of LNA modifications in the 5’ flank has a stronger effect on its toxicity than the amount of modifications in the 3’ flank.

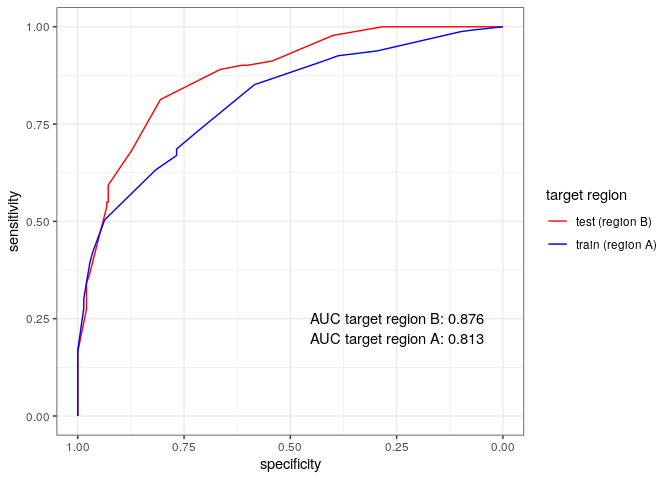
Below are the ROC curves of each region with their respective AUC scores:

# python

tabP["pred"] = best_model.predict(tabP)

# R
tabpred = py$tabP
train = dplyr::filter(tabpred, target=='A')
test = dplyr::filter(tabpred, target=='B')

rocobj = list(roc(test$too_toxic, test$pred),
              roc(train$too_toxic, train$pred))
AUCs <- sapply(rocobj, function(x) auc(x))

ggroc(rocobj)+
  theme_bw()+
  scale_color_manual(values = c('red','blue'),
                     labels = c('test (region B)','train (region A)'))+
  guides(color=guide_legend(title='target region'))+
  annotate('text', x=rep(0.25,2), y=c(0.25, 0.2),
           label = paste('AUC target region', c('B:','A:'),signif(AUCs, 3)))

← Preventing the Honeybee Apocalypse (QSAR)Covid-19 vaccination RNA dataset. →